Combining Utility AI and MCTS
Maciej Świechowski, QED Games
Introduction
In this post, you will learn:
- How AI-driven bots were created in a turn-based tactical game, in which each player controls a squad of units
- How to combine two AI algorithms in one solution: Utility AI and Monte Carlo Tree Search
The post originates from the idea to summarize information published during IEEE Symposium Series on Computational Intelligence held in Orlando (USA) in 2021:
M. Świechowski, D. Lewiński and R. Tyl, „Combining Utility AI and MCTS Towards Creating Intelligent Agents in Video Games, with the Use Case of Tactical Troops: Anthracite Shift,” 2021 IEEE Symposium Series on Computational Intelligence (SSCI), Orlando, FL, USA, 2021, pp. 1-8, DOI: 10.1109/SSCI50451.2021.9660170.
Link to the publication: https://ieeexplore.ieee.org/abstract/document/9660170
Prerequisites
We assume familiarity with the two algorithms: Utility AI and Monte Carlo Tree Search. If you want to learn more about them, we point out sources below:
Monte Carlo Tree Search (MCTS)
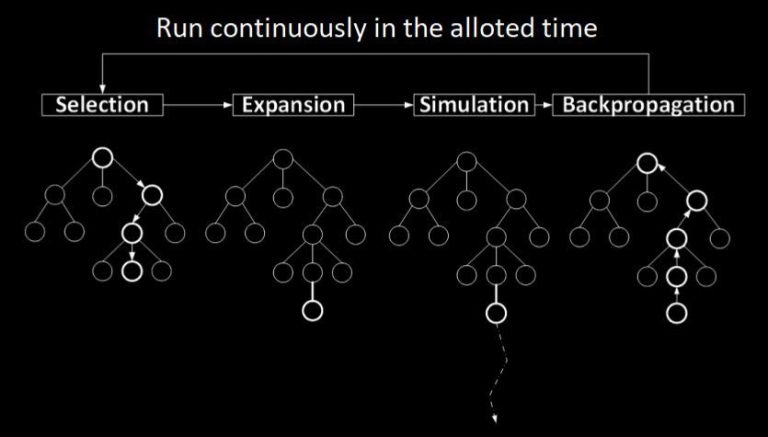
MCTS is an iterative algorithm based on simulations. This is why we call this approach “Simulated Games” in Grail. Either full game simulations (to the end) are performed or only up to a certain moment in which it is possible to introduce a function that evaluates how well players played in this particular game. Full game simulations simply use the outcome/score of the game.
During these simulations, various possibilities are tested and the statistical evidence is stored about how good particular action sequences are.
For more information about this algorithm, we recommend:
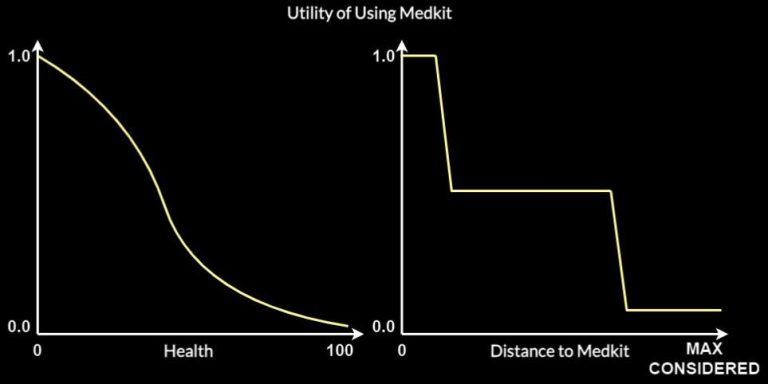
Utility Systems can be relatively complex – they can contain many curves, considerations and aggregations. The goal is to compute the utility of available actions based on which the final action selection happens.
For more information about this algorithm, we recommend:
About the game – Tactical Troops
Key features:
- 2D tactical game
- players control squads of up to 4 units
- available unit types: assault, heavy, scout and support. There can be duplicates in a squad e.g. 2x assault and 2x heavy
- continuous movement without grid
- physics instead of RNG
- 30+ weapons (rifles, machine guns, SMGs, launchers, plasmas, shotguns, sniper rifles)
- 25+ gadgets (armors, cloaks, grenades, mines, shields, stimulants)
- overwatch stance
- action points
- dynamic environment
- teleportation
- two game modes
Two games modes:
- Devastation: destroy all enemy generators. The generators are the only type of building players may have and are essentially only for the purpose of this game mode.
- Domination: capture the majority of control points, which are special circular areas on the map, and hold them for a turn
Please note that if a player eliminates or enemy units, the win is guaranteed, because there is nobody to stop the player from destroying all generators or capturing all control points.
The game modes define victory conditions, which is essential to designing AI – these are goals which bots also have to pursue.
High level architecture
In games that require complex AI, it is a good practice to introduce modularity. Good modules will have well-defined and isolated communication mechanisms. This makes the workflow easier as one can focus on each problem individually (addressed by the particular module). As long as everybody adheres to the API designed for the interaction between the modules, they are good to go.
In Tactical Troops, we introduced a three-layered architecture:
- Strategic layer – global situation assessment and basic coordination between the units. Driven by the Utility AI algorithm.
- Tactical layer – actual decisions where to position a unit and how to shoot (direction, weapon) or use gadgets. Driven by the MCTS algorithm.
- Unit layer – pathfinding, avoidance (of mines, friendly fire, obstacles), overriding orders when really required based on emergent local situation and micro-positioning when ending the turn (trying to end in a safe spot). For the scope of this post, we will not go into details here. The main reason behind a separate unit layer is computational performance. In theory, the tactical layer could address these problems but the run-time performance would not be acceptable on the current hardware.
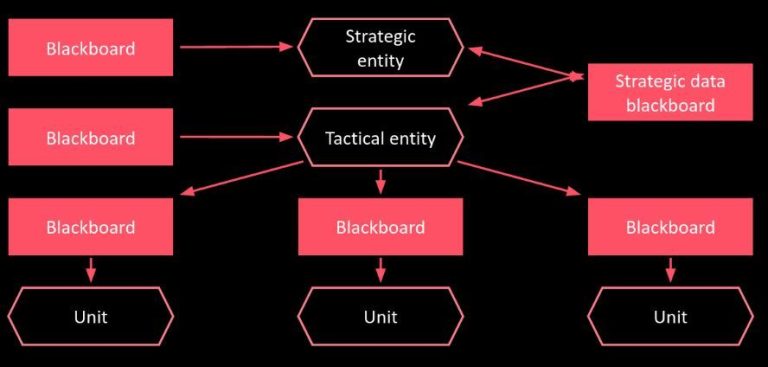
Strategic and tactical entities are instances of a component called Reasoner in Grail. The communication between them is possible thanks to blackboards. A blackboard is a generic container for data that can be written to and read from. Entities have their own private blackboards but, in addition, the strategic and tactical ones communicate using a dedicated shared blackboard.
Communication: the strategic layer chooses high-level actions for units using Utility AI. These high-level actions can be viewed as orders. They are written to the shared blackboard. Next, the tactical layer runs MCTS with an evaluation function that takes into consideration the fulfillment of those orders.
Strategic Layer: Utility AI
The strategic layer AI is executed first during the bot’s turn. The goal is to assign an order (a high level action) to each unit.
The choice of orders is an arbitrary design decision. We settled with the following ones:
- Assault POI – sends a unit on a mission of taking over the provided POI The selected unit should first try to eliminate enemies standing inside the bounds of considered area or get rid of enemies able to take control of that POI.
- Defend POI – sends a unit on a mission of making it harder for enemy to take control over POI currently held by AI player.
- Attack Generator – the selected unit should actively seek out means of destroying provided opponent’s generator.
- Rush to Point – orders a unit to prioritize going to a certain point over going on offensive.
- Ambush Envoy – orders a unit to eliminate an opponent’s unit which likely was ordered to gain control over POI or destroy a generator.
- Killing Spree – a unit that is assigned this behavior has one task – eliminate as many enemy units as possible
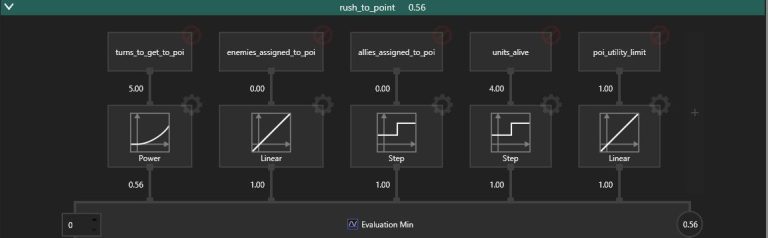
Each order is evaluated based on a number of considerations as shown in Fig. 6:
The list of possible considerations is shown in the table below. They are building blocks from which the computation of the utilities of actions is performed. Not all considerations are used for every action.
- Turns to Get to POI – the distance from a unit to a considered POI, divided by the movement range of this unit.
- Allies Assigned To POI – the number of units which have already been assigned behaviors of Rush To Point, Assault POI or Defend POI, with a given POI as parameter.
- Constant = 0.1 – this consideration is needed to assure that at least one behavior will always be chosen
- Units Alive – the number of alive allied units
- Turns To Get To Enemy – the distance from the unit to a considered enemy divided by the movement range of the unit
- Enemy Turns To Closest POI – the distance from an enemy unit to closest neutral or opponent POI as a number of turns
- Enemies Assigned To POI – the number of enemy units predicted to be willing to take over the considered POI
- Assigned Unit Advantage – a difference between Allies Assigned To POI and Enemies Assigned to POI
- Enemy Units Alive – the number of enemy units alive
- POI Utility Limit – a self-imposed limit of a score of POI-related behaviors to prevent overcommitment
(2) Evaluate the utility of each combination (type of order, available order’s parameterization) for all units
(3) Sort the tuples based on the utility
(4) While there are units with unassigned orders left:
a. Assign the (order, parameters) to a unit with the highest utility
b. Remove all tuples with this unit
c. Write the order to a shared blackboard (See Figure 4).
Tactical Layer: MCTS
Simulation-based methods are often very strong and useful but they require significant time and/or computational resources. Even if the MCTS is only launched once per player’s turn (at the beginning of it) in contrast to running continuously, we were still limited by the facts:
- Turns should not take too long. We wanted to limit the initial AI thinking time each turn, during which it looks as if nothing is happening visually, to 5-10 seconds
- The algorithm has to run on the consumers’ hardware. Therefore, no highly multi-CPU servers could be employed as it is often the case in professional or research scenarios.
There are multiple factors influencing the complexity, but the main one is continuous space and freedom of movement. The MCTS algorithm is traditionally applied to board games with very limited available positions, which is not the case here.
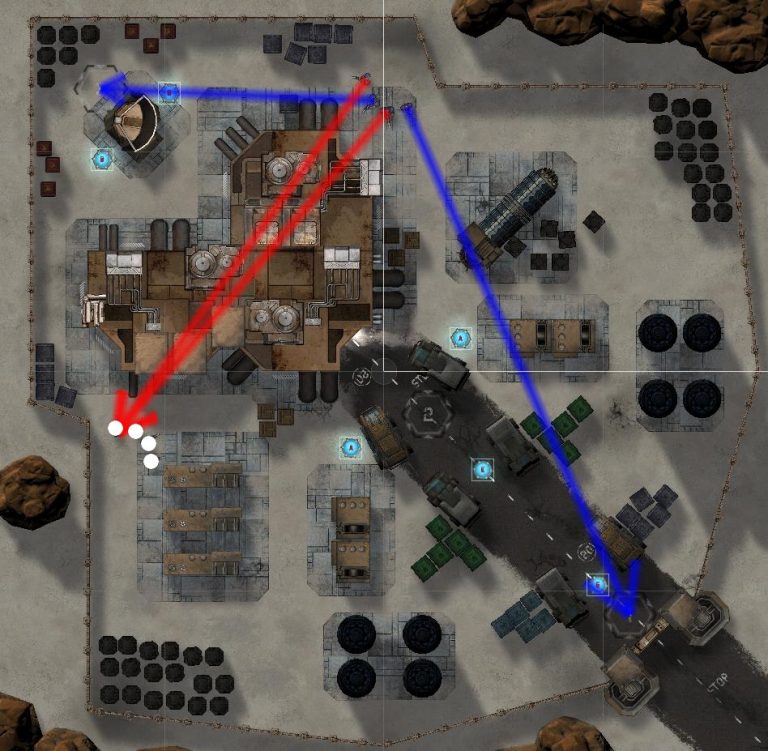
We started from sampling the maps in order to build a graph of available sensible positions for units. Such graph would be dynamically trimmed by e.g. removing nodes, in which there is too much threat for the units:
However, although the movement itself on such graphs could be handled by MCTS in reasonable time, adding more options to consider such as shooting and using gadgets was too much to compute given the imposed time constraints. Therefore, we pursued a different approach called Tactical Paths.
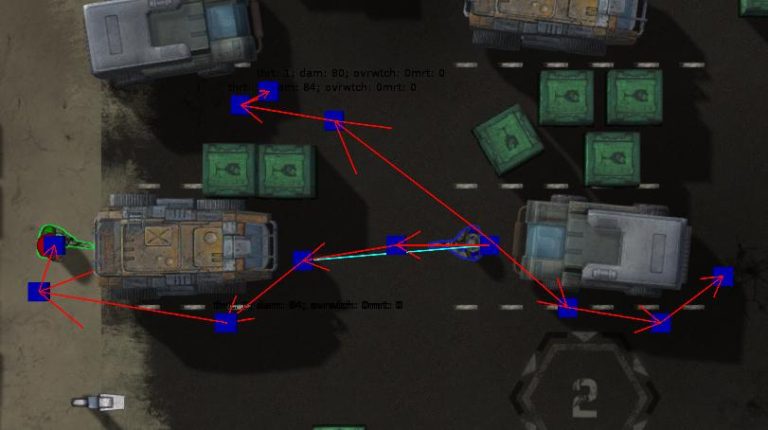
Tactical Paths
The idea is to generate a couple of candidate paths to consider for each unit. The figure below shows an example:
This is done as follows:
- For each unit, observe the distance to the target associated with the order assigned by the Strategic layer
- Find the shortest path to the target using A* on the dense navigation graph
- For each alternative path: run A* again with penalty for traversing nodes near the already computed paths
- Downsample each path by removing nodes situated too close to others on the same path. This will lead to paths with a reasonable number of key points as shown in blue in Figure 8. Such points will be called Tactical Points.
Game Tree
Now associate each Tactical Point with a state for the purpose of MCTS. Such states are nodes in the game tree constructed by the algorithm.
For example – if a unit moves from its current position to the next tactical point then it results in a new state.
However, there are more states possible than just positions on the map. In each tactical point, we consider additional actions such as shooting, throwing grenades or capturing control points (when the point happens to be inside the control point area).
These are determined by heuristics such as:
- if there is a line of sight to an enemy unit
- if our unit has high probability of destroying the enemy unit OR it will have enough action points to go to a safe position after the offensive action
For the purpose of MCTS, the game state is represented by:
• Tactical positions that the units of the AI player can go to, along with associated sets of available actions
• Internal states of each player’s units such as their current tactical position, max and current health points, max and current armor points
• In Devastator game mode: internal states of destructible targets (their health points)
• In Domination game mode: assignment of tactical positions to control points.
It means that if something from the above changes, e.g. a unit loses health points, then it means that there is a new game state for the purpose of the MCTS model.
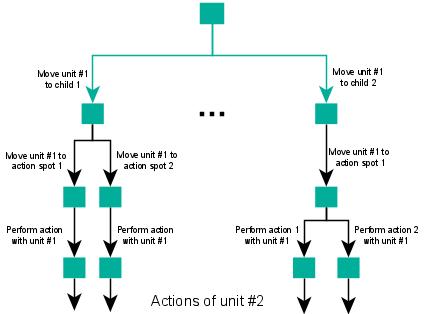
The MCTS game tree will contain actions performed by various units. The more iterations, the more possibilities will be tested. Please see Figure 9 below that shows a tree that first contains actions of unit #1 and then actions of unit #2 and others will follow:
In Tactical Troops: Anthracite Shift, units may perform actions in any order during a turn. This leads to a combinatorial explosion of options. However, often the end result of a turn is the same regardless of the order of execution. To mitigate the problem of combinatorial complexity, we do the following:
(1) Units are sorted in a greedy fashion based on the following rationale:
a. Units of type “Support” have the lowest priority
b. Units that can perform a non-movement action first (with the least amount of walking) have the highest priority
c. Tie-breaker: units with shorter tactical paths, measured by the total accumulated distance, have higher priority
(2) The game tree expansion and simulations assume the ordering as in (1)
(3) Whenever a unit makes a non-movement action, all units that did not end their turns are sorted again
Evaluation function
We limited the simulation horizon in the MCTS algorithm to a single turn. This is a trade-off between how far we can simulate the future vs. how many simulations we can perform in the very limited time. The more simulations => the more samples => the more accurate statistics. The longer simulations => the more accurate evaluation of each individual sample.
The classic MCTS runs simulations until the end of game and fetches the actual game results such as win/draw/loss. This is not feasible, therefore we introduced the evaluation function that acts as the prediction of the game result.
The evaluation function is a weighted sum of the following components:
(1) Damage score – a reward for total estimated damage dealt by AI player’s units.
(2) Game mode score – a reward for completing the current game mode’s objectives, namely destroying targets in Devastator mode or capturing control points in Domination mode.
(3) Safety score – a penalty for staying in positions threatened by enemy units, based on total estimated damage received from enemies in the following turn.
(4) Shield use score – a reward for using shields in positions threatened by enemy units or a penalty for using shields where no threats can be blocked.
(5) Overwatch stance score – a reward for using overwatch stances that have a chance of neutralizing projected threats from enemy units or a penalty if using the overwatch stance has no chance of preventing enemy attacks.
(6) Strategic order score – a bonus for following the orders of Strategic AI. Factors such as distance to goal position and damage dealt to specific attack targets are taken into account.
(7) Additional action scores – small bonuses for actions such as reloading.
(8) Huge additional bonus for winning the game.
Putting it all together
A bird’s eye view of the complete tactical layer procedure is as follows:
(1) Wait for the Strategic AI to finish computation.
(2) Assign target positions to each unit, based on orders provided by the Strategic AI and its historical positions.
(3) Construct a simplified game model for MCTS.
(4) Heuristically determine the order of unit moves.
(5) Run MCTS for a specified number of iterations.
(6) Traverse the game tree, selecting highest-scoring actions, thus building an action plan.
(7) Pass the actions to respective Unit AIs for interpretation and execution.
(8) If a recalculation event (like firing a weapon) is triggered during action execution, stop the currently executed behavior and go back to step 3.
(9) End the turn
To keep this already relatively long post shorter, we have not covered point (8). For details – please refer to the original article linked at the beginning. In short, it allows recalculating the tactical paths to update them to the current state of the environment.
Summary
In this post, we have shown how two algorithms – Utility AI and Monte Carlo Tree Search can be combined to implement a complex game AI. Tactical Troops: Anthracite Shift has been complimented for its AI despite the fact that in general the game wasn’t a big commercial success.
The combination of the algorithms has been crucial to the playing efficacy as it wins against bots that are built on one of the respective algorithms alone.
MCTS + Utility AI Player vs. MCTS Player wins 77% of games.
MCTS + Utility AI Player vs. Utility AI Player wins 97% of games.
MCTS + Utility AI Player vs. Random Player wins 100% of games.
Each experiment consisted of 200 games with players switching starting positions (first to play vs. second to play) after 100 games.
In our approach, Utility AI is responsible for the higher-level (strategic) behavior by assigning orders to units, whereas MCTS is responsible for the lower-level (tactical) execution of actions. In general, other ways of combining these algorithms are possible. For instance, MCTS could be responsible for strategic AI provided that the game model would be further simplified. Utility AI could be employed as the so-called default policy responsible for simulating the units.